Complete the two-column proof. Identify the missing statement or reason. Type the letter of your answer in each blank.
In the figure, and Prove that
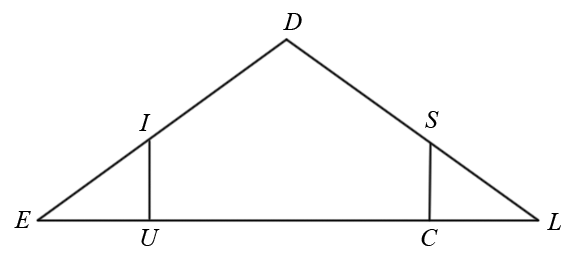
Choices:
| a. | LL Congruence Theorem |
| b. | Definition of perpendicular segments |
| c. | If two angles are supplementary and congruent, then each is a right angle. |
| d. | LA Congruence Theorem |
| e. | Linear Pair Postulate |
| f. | CPCTC |
| g. | |
| h. | and are right triangles. |
| i. | Isosceles Triangle Theorem |
Proof:
| Statements | Reasons | ||
|
1.
|
1. Given
|
||
|
2.
|
|
||
|
3.
and
are right angles.
|
|
||
|
4. Definition of right triangles
|
||
|
5.
|
|
||
|
6.
|
|


