EDGE Math 8

Type the letter of the correct justification to complete each two-column proof.

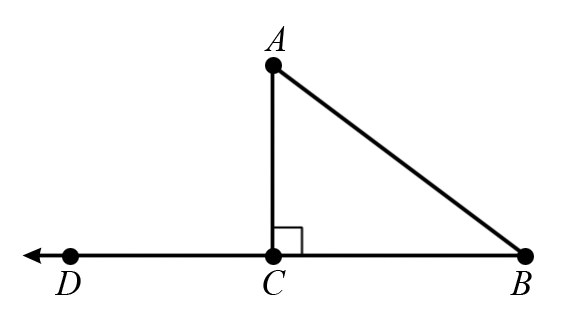
Given:	Right triangle ACB with right angle ACB
Prove:	$∠ A$ and $∠ B$ are complementary.

Choices:

a.	Definition of linear pair
b.	Substitution Property of Equality
c.	Exterior Angle Theorem
d.	Construction
e.	Subtraction Property of Equality

f.	Definition of complementary angles
g.	Definition of supplementary angles
h.	Definition of right angle
i.	Linear Pair Postulate
j.	Definition of exterior angle

Proof:

Statements

Reasons

Extend

\bar{BC}

to form

\vec{B C} .

Let point D be a point on

\vec{B C}

where C is between B and D.

∠ A C D

is an exterior angle of

Δ A C B .

m ∠ A C D

= m ∠ A + m ∠ B

∠ A C D

and

∠ A C B

form a linear pair.

∠ A C D

and

∠ A C B

are supplementary.

m ∠ A C D + m ∠ A C B

= 180 °

m ∠ A C B = 90 °

m ∠ A C D + 90 ° = 180 °

m ∠ A C D = 90 °

10.

90 ° = m ∠ A + m ∠ B

10. Statements 3 and 9, and Substitution Property of Equality

11.

∠ A

and

∠ B

are complementary.

11.

/ 10