EDGE Math 8

Refer to the figure below. Identify the postulate or theorem that supports each statement. Choose your answer.

1.	$∠ 4 ≅ ∠ 7$

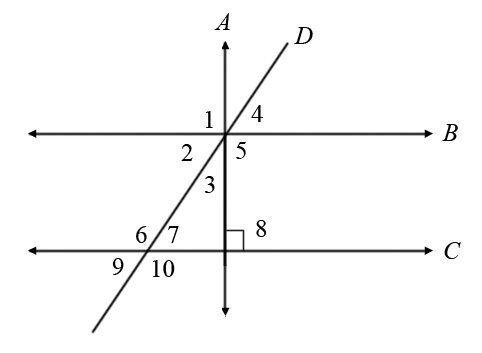
Alternate Interior Angles Theorem

Corresponding Angles Postulate (CAP)

Alternate Exterior Angles Theorem

None of the choices

Answer: Corresponding Angles Postulate (CAP)

2.	$∠ 2 ≅ ∠ 7$

Alternate Interior Angles Theorem

Alternate Exterior Angles Theorem

Same-Side Interior Angles Theorem

None of the choices

Answer: Alternate Interior Angles Theorem

3.	$∠ 4$ and $∠ 10$ are supplementary.

Same-Side Interior Angles Theorem

Same-Side Exterior Angles Theorem

Converse of CAP

None of the choices

Answer: Same-Side Exterior Angles Theorem

4.	If lines B and C are cut by a transversal D so that a pair of corresponding angles is congruent, then $B ∥ C .$

Converse of CAP

Alternate Interior Angles Theorem

Converse of Same-Side Interior Angles Theorem

None of the choices

Answer: Converse of CAP

5.	There is exactly one line parallel to line C that can contain the vertex of $∠ 4.$

Converse of Same-Side Exterior Angles Theorem

Parallel Postulate

Converse of Alternate Interior Angles Theorem

None of the choices

Answer: Parallel Postulate

6.	The shortest segment joining the vertex of $∠ 3$ to line C is the perpendicular segment.

First Minimum Theorem

Supplement Theorem

Alternate Interior Angles Theorem

None of the choices

Answer: First Minimum Theorem

/ 6