EDGE Math 8

Prove the Converse of Same-Side Exterior Angles Theorem. Identify the statement or the reason that will complete the two-column proof. Type the letter of your answer in the blank.

Given:	$∠ 1$ and $∠ 7$ are same-side exterior angles. $∠ 1$ and $∠ 7$ are supplementary.
Prove:	$l ∥ m$

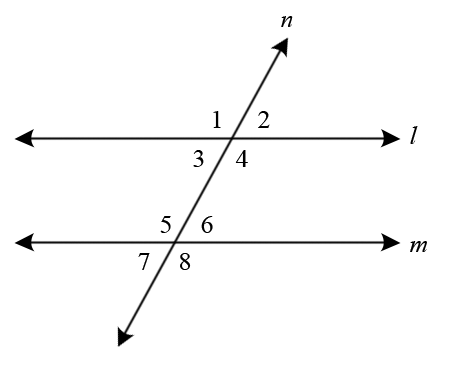
Choices:

a.	Linear Pair Postulate
b.	$∠ 2$ and $∠ 7$ are alternate exterior angles.
c.	Corresponding Angles Postulate
d.	Supplement Theorem
e.	Definition of alternate interior angles

f.	Alternate Exterior Angles Theorem
g.	$∠ 1$ and $∠ 2$ form a linear pair.
h.	$∠ 2$ and $∠ 7$ are alternate interior angles.
i.	Converse of Alternate Exterior Angles Theorem
j.	$∠ 2$ and $∠ 7$ are supplementary.

Proof:

Statements

Reasons

∠ 1

and

∠ 7

are same-side exterior angles.

∠ 1

and

∠ 7

are supplementary.

1. Given

2. Definition of linear pair

∠ 1

and

∠ 2

are supplementary.

∠ 2 ≅ ∠ 7

5. Definition of alternate exterior angles

l ∥ m

/ 5