EDGE Math 8

Identify the missing statement or reason to complete the two-column proof. Type the letter of your answer in each blank.

Given:	$∠ S T U ≅ ∠ Y R D$ $\bar{S U} ∥ \bar{R D}$ $\bar{R D} ≅ \bar{D Y}$ $\bar{S T} ≅ \bar{S U}$
Prove:	Quadrilateral SUDR is a parallelogram.

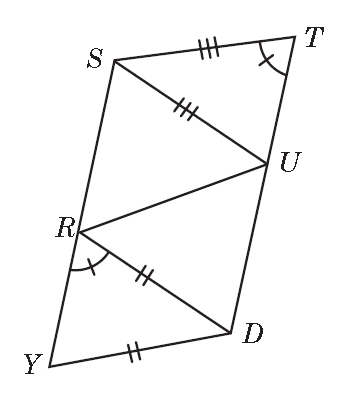
Choices:

a.	If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
b.	Corresponding Angles Postulate
c.	$∠ D R S ≅ ∠ S U D$
d.	Isosceles Triangle Theorem
e.	$m ∠ S R U = m ∠ R U D$
f.	Alternate Interior Angles Theorem

g.	If two pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
h.	Transitive Property of Angle Congruence
i.	$∠ S T U ≅ ∠ R S U$
j.	$m ∠ D R U + m ∠ S R U$ $= m ∠ R U D + m ∠ S U R$
k.	$∠ S R U ≅ ∠ R U D$
l.	Angle Addition Postulate

Proof:

Statements

Reasons

∠ S T U ≅ ∠ Y R D

\bar{S U} ∥ \bar{R D}

\bar{R D} ≅ \bar{D Y}

\bar{S T} ≅ \bar{S U}

1. Given

∠ D R U ≅ ∠ S U R

m ∠ D R U = m ∠ S U R

3. Definition of congruent angles

4. Addition Property of Equality

m ∠ D R S = m ∠ S U D

6. Definition of congruent angles

∠ Y R D ≅ ∠ R S U

∠ S U T ≅ ∠ R D U

8. Statements 1 and 7, and Transitive Property of Angle Congruence

∠ S T U ≅ ∠ S U T

9. Statement 1 and

10.

∠ R S U ≅ ∠ R D U

10. Statements 7 to 9, and

11. Quadrilateral SUDR is a parallelogram.

11. Statements 6 and 10, and

/ 11