EDGE Math 8

Identify the missing statement or reason to complete the two-column proof. Type the letter of your answer in the box.

Given:	Quadrilateral ABCD is a parallelogram. Quadrilateral BCEF is a parallelogram.
Prove:	Quadrilateral AFED is also a parallelogram.

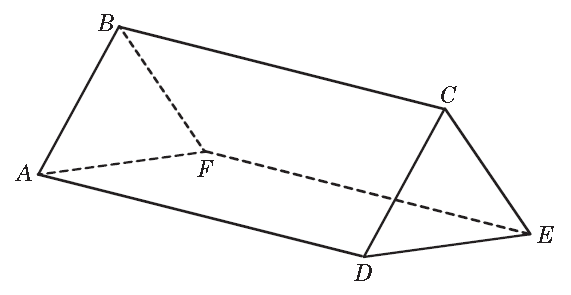
Choices:

a.	CPCTC
b.	$\bar{AD} ≅ \bar{FE}$
c.	Definition of parallelogram
d.	Opposite sides of a parallelogram are congruent.
e.	If two sides of a quadrilateral are parallel and congruent, then the quadrilateral is a parallelogram.

f.	Converse of Same-Side Interior Angles Theorem
g.	$\bar{BC} ≅ \bar{FE}$
h.	Two lines parallel to the same line are parallel.
i.	$\bar{BC} ∥ \bar{FE}$
j.	If one angle of a quadrilateral is supplementary to both angles adjacent to it, then the quadrilateral is a parallelogram.

Proof:

Statements

Reasons

1. Quadrilateral ABCD is a parallelogram.
Quadrilateral BCEF is a parallelogram.

1. Given

\bar{AD} ∥ \bar{BC}

and

\bar{A D} ∥ \bar{F E}

\bar{A D} ≅ \bar{B C}

and

5. Transitive Property of Segment Congruence

6. Quadrilateral AFED is also a parallelogram.

6. Statements 3 and 5, and

/ 7